
By Lawrence G. McMillan
This article was originally published in The Option Strategist Newsletter Volume 9, No. 05 on March 9, 2000.
Two issues ago, we wrote about the effects of changes in implied volatility on a call bull spread. Several readers asked about similar effects on other “common” positions – especially on put spreads – so we’ll expand on that theme this week
Before getting into the specific strategies, a little background on the put option itself may be useful. A put option tends to lose its premium fairly quickly as it becomes an in-the-money option. This is due to the realities of conversion arbitrage. In a conversion arbitrage, an arbitrageur or market maker buys stock and buys the put, while selling the call. If he carries the position to expiration, he will have to pay carrying costs on the debit incurred to establish the position. Furthermore, he would earn any dividends that might be paid while he holds the position. In a “perfect” world, all option prices would be so accurate that there would be no profit available from a conversion. That is, the following equation (1) would apply:
(1) call price + strike price – stock price – put price + dividend – carrying cost = 0
where carrying cost = strike price / (1 + r)t
and t = time to expiration
r = interest rate
Now, we also know that the time value premium of a put is the amount by which its value exceeds intrinsic value. The intrinsic value of an in-the-money put option is merely the difference between the strike price and the stock price. Hence one can write the following equation (2) for the time value premium (TVP) of an in-the-money put option:
(2) Put TVP = put price – strike price + stock price
The arbitrage equation from page 1 can be rewritten as:
(3) Put – strike + stock = call + dividends – carrying cost
and substituting equation (2) for the terms in equation (3), one arrives at:
(4) Put TVP = call + dividends – carrying cost
In other words, the time value premium of an in-themoney put is the same as the (out-of-the-money) call price, plus any dividends to be earned until expiration, less any carrying costs over that same time period.
Assuming that the dividend is small or zero (as it is for most stocks), one can see that an in-the-money put would lose its time value premium whenever carrying costs exceed the value of the out-of-the-money call. Since these carrying costs can be relatively large (the carrying cost is the interest being paid on the entire debit of the position – and that debit is approximately equal to the strike price), they can quickly dominate the price of an out-of-the-money call. Hence the time value premium of an in-the-money put disappears rather quickly.
This is important information for option buyers because they must understand that a put won’t appreciate in value as much as one might expect, even when the stock drops, since the put loses its time value premium quickly. It’s even more important information for put sellers: a short put is at risk of assignment as soon as there is no time value premium left in the put. Thus, a put can be assigned well in advance of expiration – even a LEAPS put!
Now, returning to our main topic of how implied volatility affects a position, one can ask himself how an increase or decrease in implied volatility would affect equation (4) above. If implied volatility increases, the call price would increase – and if the increase were great enough – might impart some time value premium to the put. Hence an increase in implied volatility also may increase the price of a put, but if the put is “too far” in the money, a modest increase in implied volatility still won’t budge the put. That is, an increase in implied volatility would increase the value of the call, but until it increases enough to be greater than the carrying costs, the put will remain at parity and thus a short put would still remain at risk of assignment.
Bull Spread
One of the more popular strategies involving puts is the sale of a credit spread – a bull spread with puts. Assume that a stock is selling at 100, and one is going to sell a put with a 110 strike and buy a put with a 90 strike. That is a put credit (bull) spread. Also assume that the options have 4 months of life remaining.
| Implied Volatility | Put Bull Spread (Theo. Value) |
| 20% | 9.15 cr * |
| 30% | 9.70 cr |
| 40% | 10.12 cr |
| 50% | 10.46 cr |
| 60% | 10.78 |
| 70% | 11.05 |
| 80% | 11.33 |
One would not rationally sell this credit spread if implied volatility were as low as 20% because at that low level of volatility, the in-the-money Dec 110 put is trading for 10 dollars – parity – and thus would immediately be at risk of early assignment. But one can see that an increase in implied volatility increases the value of the spread. Now, if one had sold this spread to begin with, he would thus be losing money when implied volatility increased. This is what we proved with call bull spreads, too – they lose money when implied volatility increases.
What happens after 30 days have passed? The following graph shows just two cases – implied volatility at 30% and implied volatility at 80%. One can surmise that other levels of implied volatility between 30% and 80% would have profit graphs that lie between the two shown below.
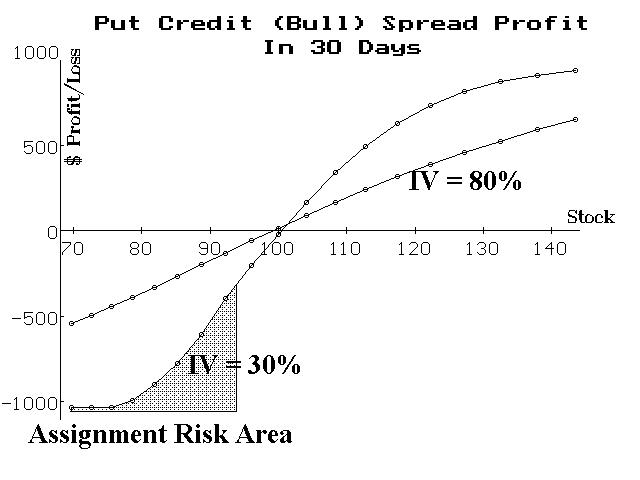
First, one can observe that a bull put spread does not widen out to anywhere near its maximum potential if implied volatility increases. We saw the same thing with the call bull spread in the previous article. But a put bull spreader is caught in another “trap”: if implied falls and the stock falls, too, the risk of early assignment materializes quicky.
Note the shaded area at the lower left of the graph – extending from a price of about 94 on down. After 30 days (so there would be three months life remaining at that point in time), if implied volatility is 30%, the 110 put (the short put) would be trading at parity for stock prices of 94 and below. Thus, it would be at risk of early assignment. If implied volatility were even lower, the puts would be at parity for much higher stock prices.
Now, in and of itself, early assignment on an equity or futures put spread is not really a terrible thing. Yes, there will be a request for additional margin (because the stock has to be paid for or the futures contract margined), but the risk is still the same in dollar terms. Of course, the request for extra margin could be back-breaking for a stock trader, and the early assignment would probably incur additional commission costs, too. However, with cash-based index options there is a serious increase in risk after an early assignment, because one is left only with the other side of the spread (the long put option, struck at 90). If that option happens to have substantial value, then you have considerable risk if the underlying should quickly move higher. In fact, by the time you unwind the spread, you might actually end up losing more than your original “limited” risk amount – all due to the early assignment (this could happen if the underlying first plunges in price – placing both options deeply in-the-money, after which you get assigned on the short put option, followed by the underlying then dramatically rising in price).
The lesson that I would take from this example is this: if one is considering using bull spreads where at least one of the options is at- or in-the-money, then a call bull spread is a superior choice over a put bull spread. Early assignment is not really a consideration for most call spreads.
In both cases, however, a more serious problem exists and that is that the spread does not widen out much even when the stock makes a nice bullish move for you. Thus, it is actually better to buy a call option in most cases than to use the bull spread, because profits are larger and an increase in implied volatility is a favorable thing for an outright call buyer.
Note that these effects are similar, but much less pronounced for out-of-the-money put credit spreads. Still, it should be noted that an increase in implied volatility will harm an out-of-the-money put credit spread, too. Hence if the underlying goes into a rapid fall (crash, plunge) then implied volatility usually increases quickly and dramatically. So, an out-of-the-money credit spreader is hit with the double whammy of expanding implied volatility and the fact that the underlying is fast approaching the strike price of his options, thereby expanding the price of the spread.
Bear Spreads
What about the put spread in a bearish situation? In this case one buys the put with the higher strike and sells the put with the lower strike to construct a simple put bear spread. Actually, a sudden increase in implied volatility is of help to the bear put spread. That is, the spread will widen out slightly. To verify this, look at Table 1 again. Only now imagine that we are buying the spread for a debit. Note that the smallest debit is at the lower implied volatility – 9.15 debit with IV at 30%. If implied volatility were to “instantaneously” jump to 80%, the spread would widen out to 11.33 debit. A very quick profit could be had. So there’s a difference right away between a debit call bull spread (which loses money when implied volatility suddenly increases) and the debit put bear spread.
Unfortunately, the other major drawback – that the spread doesn’t widen out much if the underlying makes a favorable move – is still true. The following profit graph shows a bear put spread, 30 days hence, for two different implied volatilities. Once again, the lower volatility spread widens out more quickly because both options tend to go to parity in that case. In fact, one can see on the graph that there is early assignment risk in the low volatility case, below a price of about 77 on the stock. That is not a problem, though, since the spread would have widened to its maximum potential in that case and could just be removed when the risk of early assignment materialized. When implied volatility remains high, though, the spread doesn’t widen out much, even when the stock drops a lot after 30 days. Since it is common for implied volatility to rise (even skyrocket) when the underlying drops quickly, the put bear spread probably won’t widen out much. That may not be a psycho-logically pleasing strategy because you won’t make the level of profits that you had hoped to when the underlying fell quickly.
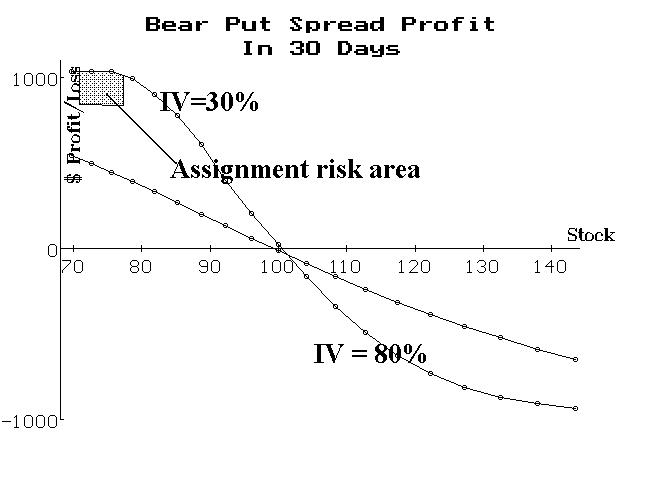
Once again, it seems that the outright purchase of an option is probably superior to a spread – in these cases, it is true with respect to puts, much as it was with call options in the newsletter of a month ago. Spreading often unnecessarily complicates a trader’s outlook.
This article was originally published in The Option Strategist Newsletter Volume 9, No. 05 on March 9, 2000.
© 2023 The Option Strategist | McMillan Analysis Corporation

